Nun gut. Ich komme so langsam in meinem studentischen Leben an einen Punkt, wo ich Vorlesungen aus einer etwas zurückgezogenen Position betrachte und von dort die Vorlesungen also nicht gerade kritisch betrachte, sondern stellenweise aus anderen Blickwinkeln als früher. Und so habe ich in den letzten Wochen mal ein kleines Experiment gewagt. Ich versuche Beziehungen in einer Vorlesung anhand von kleinen Zeichnungen oder Sprüchen zu versehen. Das interessante ist, man kann somit schnell visuelle Eselsbrücken bauen und man kann das Hirn ein wenig kreativer verwenden. Ich hoffe mal, dass das für die spätere Klausurenrunde helfen kann.
Hier mal ein paar Beispiele aus Differential Geometric Aspects of Image Processing:
Die dritte Ableitung eine Kurve wird auch die Torsion tau(s) genannt. Also kam mir folgende Abkürzung in den Sinn:
Dann eine Grundidee der Differentialgeometrie: Man versucht Topologische Räume mit Mannigfaltigkeiten abzubilden. Ein Beispiel hierfür ist die Darstellung der Erde mit den bekannten Höhenlängen und Breitengraden, die dann auf eine dreidimensionale Abbildung gemappt werden. 
Wenn es dann halt um Oberflächen geht kann man folgende Definitionen machen… Eine reguläre Oberfläche, eine Normalfläche und eine Tangentialfläche. Die Reguläre Fläche ist so ähnlich wie ein Tennisplatz und die Normalfläche das Netz in der Mitte. Eine Tangentialebene ist in etwa ein Bumper Sticker, den man am Auto befestigt und sich an die Oberfläche des Autos schmiegt.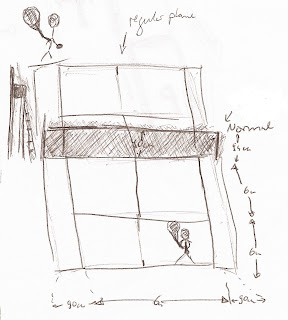

Ach ja… es gibt dann ja noch den Unit Circle… Hier als Polizeiabzeichen…
joa… sonst gibts halt noch eine Assoziation, dass die erste und zweite Fundamentalform I und II einer Sphäre identisch sind…
Ach ja… und hoffen wir mal dass die folgenden Vorlesungen nicht von mathematischen Piraten geentert werden wird… deren Ruf schallt schon aus weiter Entfernung…